Does Volume Depend on Time?

Problem

A first-order reaction $(A \rightarrow products)$ takes place in an aqueous solution. At the same time, while $A$ is converting into products, the water in the solution is evaporating. The decrease of the solution volume is described by the equation: $V(t) = V(t=0) - \alpha t$. Does the concentration of reagent A increase or decrease in the solution over time?

Solution

To begin with, we need to understand the idea itself. What does it mean for a concentration to increase or decrease over time? This is simply a question about determining the monotonic behavior of a function: $C=f(t)=C(t)$. There are multiple ways to approach this.

For example, suppose we want to check whether the concentration increases. Then we might compare values such as $C(t+1) > C(t)$: if at a later time the concentration is higher, the function is increasing. However, this approach is not always reliable and can fail to give the correct result.

A much simpler and more powerful method is to examine the sign of the first derivative. Why does this work? Let’s recall the definition of a derivative: $$\frac{dC(t)}{dt}=\lim_{\Delta t\to \infty}\frac{C(t+\Delta t)-C(t)}{\Delta t}$$

Oops, right — earlier we only looked at the case where the function is increasing, meaning $C(t + \Delta t) > C(t)$. Here we have the same type of inequality, and it’s true when $\Delta t > 0$. So if the derivative is positive, the concentration is growing. You can show the same thing for a decreasing function too (just check the case $\Delta t < 0$ yourself). Okay, now let’s actually get back to the problem. We need to find the explicit form of the concentration $C(t)$. We already know the volume $V(t)$, but we don’t know the amount of substance $n(t)$ yet. So we’ll use the law of mass action. It gives us: $$r(t)=-\frac{1}{V(t)}\frac{dn(t)}{dt}=\frac{1}{V(t)}kn(t)$$

But wait a second. Since the volume depends on time, we can’t just hide it inside the derivative. Instead, let’s multiply both sides of the equation by $V(t)$: $$-\frac{dn(t)}{dt}=k n(t)$$ This is the usual differential equation for a first-order reaction. It’s really easy to integrate: $$\int^{n(t)}_{n(0)}\frac{dn}{n}=\int^{n(t)}_{n(0)}d(\ln{n})=-k\int^{t}_{0}dt$$ And after integrating, we get the classic exponential decay: $$n(t)=n(0)\cdot e^{-kt}$$ Now we finally have a clean expression for the concentration, since $$C(t)=\frac{n(t)}{V(t)}=\frac{n(0)\cdot e^{-kt}}{V(0)-\alpha t}$$ Lets take the derivative: $$\frac{dC(A)}{dt}=\frac{d}{dt}(\frac{n(t=0)\cdot e^{-kt}}{V(t=0)-\alpha t})$$ $$\frac{dC(A)}{dt}=\frac{-k\cdot e^{-kt}\cdot n(t=0)(v(t=0)-\alpha t)+\alpha\cdot e^{-kt}\cdot n(t=0)}{(V(t=0)-\alpha t)^2}$$ The square, the exponential, and the initial number of moles are all positive quantities. Therefore, the sign is determined by only one bracket: $$\alpha kt-kV(t=0)+\alpha\lor 0$$ Let us consider the case of increasing concentration: $$\alpha kt-kV(t=0)+\alpha\ge 0$$ $$t\ge\frac{V(t=0)}{\alpha}-\frac{1}{k}=\frac{kV(t=0)-\alpha}{\alpha k}$$ From this, two situations become clear

1) $\alpha>kV(t=0)$. In this case the fraction is negative, and since time is a non-negative quantity, this inequality will hold for any $t$. Let’s plot the graph for specific values: $C(t) = exp(-t)/(1 - 2t)$

2) $kV(t=0)>\alpha$ In this case the situation is less straightforward. Let’s plote the graph using specific numerical values: $C(t)=exp(-t)/(1-0.5t)$

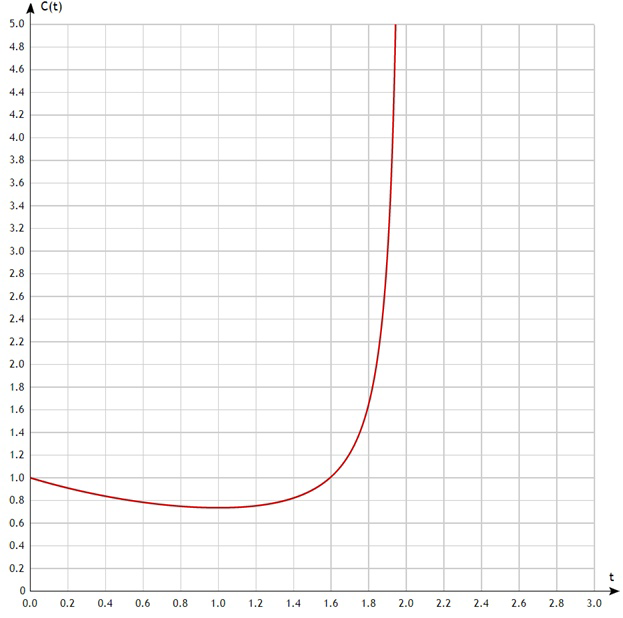
That is, at first the concentration decreases and then, after the inflection point, it begins to increase.